-
Eigenfrequency
고유 주파수
-
임의의 계의 고유 진동수(natural frequency)를 의미하며, 유사한 용어로 공진 주파수(resonant frequency)가 있다. 엄격한 의미에서 공진 주파수와 고유 주파수는 동일하지 않으며, 고유 주파수는 수학적으로 고유치 문제(eigenvalue probrem)로부터 정의되고, 공진 주파수는 물리적 입장에서 가진 주파수와 고유 진동수가 일치할 경우 나타나는 물리적 의미로 정의된다. 참고) 고유치 문제
-
Eigenvalue Problem
고유치 문제
-
일반적으로 물리계를 수학적으로 표현하면, 많은 경우 다음과 같은 고유치 문제로 표현할 수 있다.
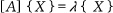
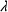 는 고유치(eigenvalue), {X}는 고유 벡터(eigenvector)를 의미한다. 고유치 문제는 수학적으로 행렬 [A]로 벡터 {X}를 선형변환(즉, rotation과 scaling)시켰을 때, 원래 벡터 {X}의 방향을 가리키는 가중치
는 고유치(eigenvalue), {X}는 고유 벡터(eigenvector)를 의미한다. 고유치 문제는 수학적으로 행렬 [A]로 벡터 {X}를 선형변환(즉, rotation과 scaling)시켰을 때, 원래 벡터 {X}의 방향을 가리키는 가중치 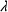 와 벡터 {X}를 찾는 문제로 설명된다.
와 벡터 {X}를 찾는 문제로 설명된다.
진동계의 예를 들면, 고유치는 계의 고유 진동수를, 고유 벡터 {X}는 계의 모드 현상을 의미한다. 위와 같은 이유로 수학적으로 정의된 고유치와 고유 벡터에 물리적 의미를 부여하여 고유 주파수(eigenfrequency) 또는 고유 모드(eigenmode)라고도 부른다. -
Elastic Modulus
탄성 계수
-
Ela임의의 재질의 탄성 특성을 나타내는 척도로서 재질 내 임의의 공간 위치와 시간에 대하여 응력과 변형률 사이의 비례계수로 정의된다. 즉 단순 인장의 경우,
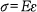
여기서 는 응력,
는 응력,  은 변형률,
은 변형률, 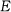 는 종탄성계수(Young 계수)를 의미한다.
는 종탄성계수(Young 계수)를 의미한다.
많은 경우에 있어서 단순 조화 운동에 대하여 탄성 계수는 시간항을 제외한 공간의 함수로 표현된다.
-
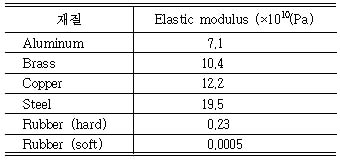
Elasticity
탄성
-
임의의 재질에 가해지는 응력(stress)의 크기에 따라 발생되는 변형률(strain)
 정도의 비를 의미하는 일반적인 용어이다. 가해지는 응력의 크기가 작아 단순비례 관계가 성립하는 경우, 재질은 탄성영역에 있다고 말한다.
정도의 비를 의미하는 일반적인 용어이다. 가해지는 응력의 크기가 작아 단순비례 관계가 성립하는 경우, 재질은 탄성영역에 있다고 말한다.
-
Encorder
엔코더
-
병진 또는 회전 운동체의 변위, 속도 및 가속도를 측정하는 장치로서, 2진화된 이산 신호 형태의 출력을 통해서 알고 싶은 물리량을 측정할 수 있다. 계측하고자 하는 운동 형태에 따라 병진형(translationa type) 엔코더와 회전형(rotary type) 엔코더로 구분된다.
-
Energy Spectral Density(ESD)
에너지 스펙트럼 밀도
-
임의의 신호
.jpg) 에 대한 에너지 스펙트럼밀도는 수집신호의 수집시간
에 대한 에너지 스펙트럼밀도는 수집신호의 수집시간 -2.jpg) 동안에
동안에 .jpg) 에 담겨 있는 에너지를 의미하며, 수학적으로 다음과 같이 정의된다.
에 담겨 있는 에너지를 의미하며, 수학적으로 다음과 같이 정의된다.
-3.jpg)
-4.jpg) 는 기대값,
는 기대값, -5.jpg) 는 신호
는 신호 .jpg) 의 유한시간
의 유한시간 -2.jpg) 에 대한 푸리에 변환값,
에 대한 푸리에 변환값, -6.jpg) 는
는 .jpg) 의 에너지 스펙트럼 밀도를 의미한다.
의 에너지 스펙트럼 밀도를 의미한다.
-
Ensemble
앙상블
-
여러 수집신호(sample record)의 집합. 랜덤 신호의 처리에서 기대값은 앙상블 영역에서의 평균으로 구해진다. 예를 들면 아래와 같이 항공기 날개 끝의 가속도 신호를 어느 항공기가 매번 항해할 때 기록하였다고 하자.
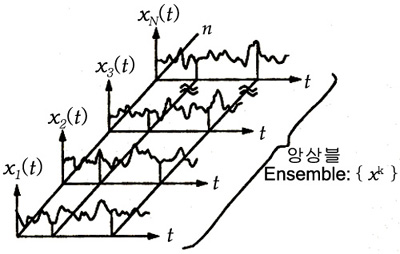
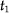 (즉 이륙후
(즉 이륙후 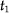 시간 후)에서의 항공기 날개 끝의 가속도
시간 후)에서의 항공기 날개 끝의 가속도 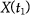 의 앙상블은
의 앙상블은 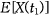 이며 그림에서 표시된 바와 같이
이며 그림에서 표시된 바와 같이
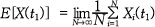
-
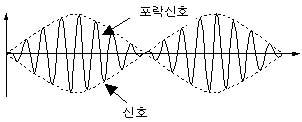
Envelope
포락(包絡), 포락선
-
임의의 신호의 최대값들을 연결하여 구성된 신호를 포락 신호(envelope signal)라 한다. 임의의 신호에 대한 포락 신호는 수학적으로 힐버트 변환(hilbert transform)등에 의해 얻을 수 있는 것으로 밝혀져 있다. 개념적인 면에서 보면
-
Equalizer
평형장치(平衡裝置)
-
원하는 주파수 대역에 걸쳐 계의 출력이 입력 신호에 대해 균일하게 응답하도록 하는 장치로서, 흔히 이산 여파기로 구성되며 사전에 신호 전달계의 특성을 알기 어려우므로 실제 출력과 원하는 출력과의 오차를 줄여나가는 적응 여파기 형태를 취한다.
-
Evanescent Wave
지수 감쇠파
-
공간에 따라 위상은 변화하지 않고 크기가 지수 함수적으로 감소(혹은 증가)하는 형태의 함수 혹은 물리량을 진행파(propagating wave)에 대응하여 표현하는 용어이다. 수학적으로는 파 진행 방향의 파수 성분이 허수가 될 때 발생한다. 예를 들면 직교 좌표계를 사용하여 3차원 공간에서 전파하는 파동의 음압을 표현하면
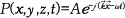
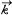 는 파동의 진행 방향 및 파수를 나타내는 파수 벡터이다. 이 파수 벡터는 다시 각각
는 파동의 진행 방향 및 파수를 나타내는 파수 벡터이다. 이 파수 벡터는 다시 각각 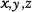 방향의 성분으로 구성되어 있는 것으로 생각할 수 있고, 즉
방향의 성분으로 구성되어 있는 것으로 생각할 수 있고, 즉
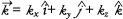
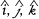 는 각각
는 각각 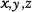 방향의 단위 벡터이다. 결국 이 파동은
방향의 단위 벡터이다. 결국 이 파동은
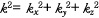
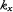 와
와 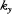 값에서는
값에서는 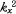 가 음수가 될 수 있고 따라서 지수 함수적으로 감소(혹은 증가)하는 파동이 있음을 이해할 수 있다.
가 음수가 될 수 있고 따라서 지수 함수적으로 감소(혹은 증가)하는 파동이 있음을 이해할 수 있다.


