사단법인한국소음진동공학회
The Korean Society for Noise and Vibration Engineering
-
Kaiser-Bessel Window
카이저-베셀 창문 함수
-
Kaiser에 의해 만들어진 창문 함수로서 다음과 같이 정의된다.
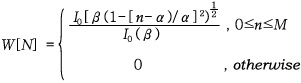
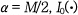 는 제 1종 영차 수정 베셀 함수(zeroth order modified bessel function of the first kind),
는 제 1종 영차 수정 베셀 함수(zeroth order modified bessel function of the first kind), 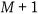 는 창문 함수 길이(window length),
는 창문 함수 길이(window length), 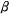 는 형상 변수(shape parameter)
카이저-베셀 창문 함수를 이용하면 창문 함수의 길이
는 형상 변수(shape parameter)
카이저-베셀 창문 함수를 이용하면 창문 함수의 길이 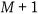 과 형상 변수
과 형상 변수 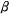 를 조절하여 여러가지 형태의 창문 함수를 구성할 수 있다.
를 조절하여 여러가지 형태의 창문 함수를 구성할 수 있다.
참고) 한(hann) 창문 함수, 해밍(hamming) 창문 함수 -
Kinetic Energy
운동 에너지
-
물체가 운동을 할 때 가지게 되는 에너지로서 그 크기는 운동을 하고 있는 물체가 정지할 때까지 할 수 있는 일의 양으로 정의한다. 일반적으로 강체가 운동할 때는 병진 운동에 의한
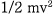 과
회전 운동에 의한
과
회전 운동에 의한 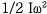 로
이루어진 운동 에너지를 가진다. 여기서
로
이루어진 운동 에너지를 가진다. 여기서 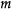 은 질량,
은 질량,  는 속도,
는 속도,  는 회전 관성 모멘트이고
는 회전 관성 모멘트이고  는 각속도이다.
는 각속도이다.
음향의 경우 단위 부피당 운동 에너지는 1/2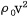 로 표현할 수 있으며 여기서
로 표현할 수 있으며 여기서 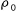 는 유체의 밀도,
는 유체의 밀도,  는 속도를 의미한다. 진동의 경우와는 달리 유체 입자의 속도 측정이 용이하지 않아 음압차를 이용한 방법을 보편적으로 사용하며 이것은 오일러 방정식(euler equation), 즉
는 속도를 의미한다. 진동의 경우와는 달리 유체 입자의 속도 측정이 용이하지 않아 음압차를 이용한 방법을 보편적으로 사용하며 이것은 오일러 방정식(euler equation), 즉
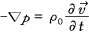
참고) 인텐시티 -
Kirchhoff-Helmholtz Integral Equation
키르히호프-헬름홀쯔 적분식
-
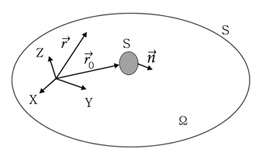
음원이 존재하지 않는 공간상의 폐영역(
 )에서의 음장은 이 영역을 둘러싸는 경계면의 경계조건과 Green 함수를 이용하여 구할 수 있으며 이를 식으로 나타낸 것이 키르히호프-헬름홀쯔 적분식으로 다음과 같이 표현된다.
)에서의 음장은 이 영역을 둘러싸는 경계면의 경계조건과 Green 함수를 이용하여 구할 수 있으며 이를 식으로 나타낸 것이 키르히호프-헬름홀쯔 적분식으로 다음과 같이 표현된다.
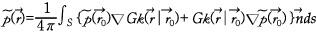
여기서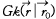 는 자유공간 그린(green) 함수로
는 자유공간 그린(green) 함수로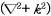
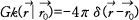 를 만족하는 함수이며
를 만족하는 함수이며 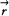 은 예측점의 위치벡터,
은 예측점의 위치벡터, 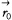 는 경계면의 위치벡터,
는 경계면의 위치벡터, 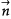 은 경계면위의
은 경계면위의 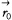 에서의 법선벡터,
에서의 법선벡터, 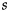 는 경계면이다.
는 경계면이다.
적분 방정식의 첫 번째 항은 음원을 포함한 경계면에서의 음압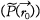 이 관측점 혹은 예측점
이 관측점 혹은 예측점 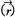 에 미치는 영향을 표현하고 있으며 두 번째 항은 역시 경계면에서의 속도와 관계 있는 음압의 공간상 변화
에 미치는 영향을 표현하고 있으며 두 번째 항은 역시 경계면에서의 속도와 관계 있는 음압의 공간상 변화 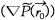 가 예측점에 미치는 혹은 전파되는 점을 반영하고 있다. 여기서
가 예측점에 미치는 혹은 전파되는 점을 반영하고 있다. 여기서  는
는 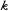 파수에 해당하는 그린 함수로서 음원으로부터 측정점 혹은 예측 지점까지의 전파현상을 표현하고 있다. 일반적으로는 시간 영역까지 확대할 수 있으며, 이 때의 키르히호프-헬름홀쯔 적분식은 다음과 같다.
파수에 해당하는 그린 함수로서 음원으로부터 측정점 혹은 예측 지점까지의 전파현상을 표현하고 있다. 일반적으로는 시간 영역까지 확대할 수 있으며, 이 때의 키르히호프-헬름홀쯔 적분식은 다음과 같다.